从物理效应到工业应用
"piezo"(压电)一词是从希腊语中的“压力”一词派生而来的。1880年,雅克•保罗•居里和皮埃尔•居里发现施加压力能在石英、电气石等多种晶体中产生电荷,他们将这种现象称为"piezoelectric effect"(压电效应)。后来,他们发现电场可以使压电材料变形。这种效应被称为"inverse piezoelectric effect"(逆压电效应)。 当科学家发现在施加电场时钛酸钡能在一个有效范围内利用压电特性,产业突破 >>便伴随着压电陶瓷而来。 压电效应目前用于点火器、扬声器和信号转换器等多种日常用品。此外,由于内燃机中的压电控制喷射阀减少了传递时间,大大改善了平滑度和废气质量,压电促动器技术也在汽车技术中得到认可。
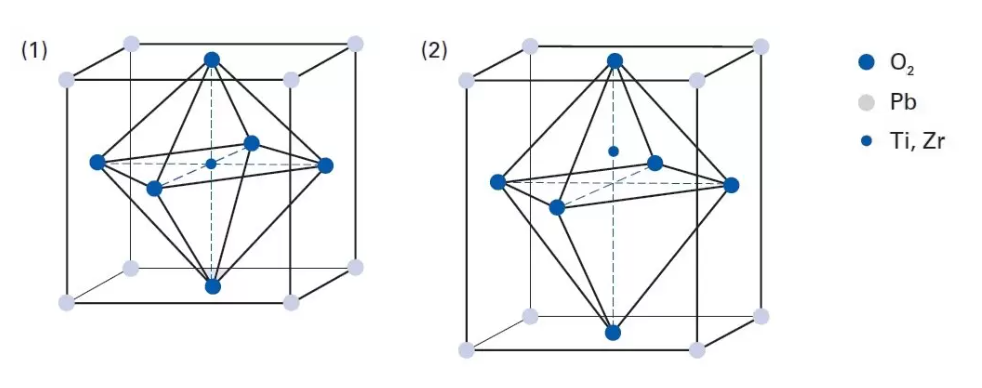
在压电材料表面施加压力可以产生电荷。这种直接压电效应,也称发电机或传感器效应,将机械能转换为电能。 反之,施加一定电压时,逆压电效应可以改变此类材料的长度。这种促动器效应将电能转换成机械能。 单晶材料和多晶铁电陶瓷中都可产生压电效应。在单晶中,晶格晶胞的不对称结构,即低于居里温度TC 时形成的极轴,是产生这种效应的充分必要条件。 此外,压电陶瓷具有自发极化特性,即晶胞的正负电荷浓度相互分离。同时,晶胞的轴线沿自发极化的方向延伸,产生自发应变。
石英、电气石和罗谢尔盐等天然单晶材料的压电效应相对较小,而钛酸钡(BaTiO3)和锆钛酸铅(PZT)等多晶铁电陶瓷表现出较大的位移或产生更高的电压。PZT压电陶瓷材料有许多种类,广泛运用于促动器或传感器应用中。PZT陶瓷中带镍、铋、镧、钕、铌等离子的特殊掺杂质可特定优化压电和介电参数。
温度低于居里温度T C 时,PZT微晶的晶格结构开始变形并变得不对称,使偶极子形成,产生菱形及正方形晶相,而这些都是压电技术的关注点。陶瓷表现出自发极化特性。温度高于居里温度时,压电陶瓷材料失去其压电性能。

极化磁畴(图:IKTS Dresden)
铁电极化
为了减少材料的内能,陶瓷微晶中形成铁电畴。铁电畴内,自发极化的方向都是相同的。 边界磁畴的不同方向由畴壁隔开。陶瓷的宏观压电还需要一个铁电极化过程。
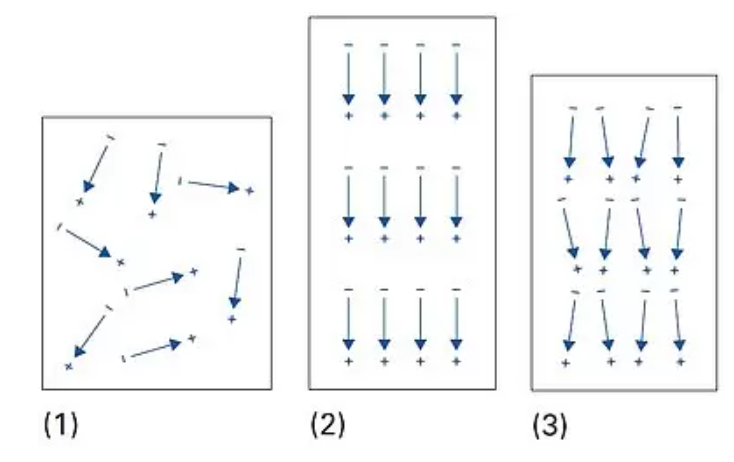
铁电极化原理
为此,必须施加一个介电强度为数kV/mm的强电场,使之前无结构的陶瓷化合物中产生不对称。电场使自发极化进行重定向。同时,向极性磁场方向有择优取向的磁畴不断扩大,其他无择优取向的则不断收缩。畴壁在晶格中被移动。 极化后,即使不施加电场,大部分重定向也会得以保存。然而,由于内部机械应力等原因,少量畴壁会被移回至原来位置。
极化压电陶瓷的膨胀

一旦施加电场,陶瓷就会膨胀,极化场强将会减弱。这种效应一部分是因为晶格中离子的压电位移,称为内在效应。 外在效应是基于晶胞的可逆铁电重定向。它随着驱动场强度的增大而增大,是铁电压电陶瓷大部分非线性迟滞和漂移特性的原因所在。
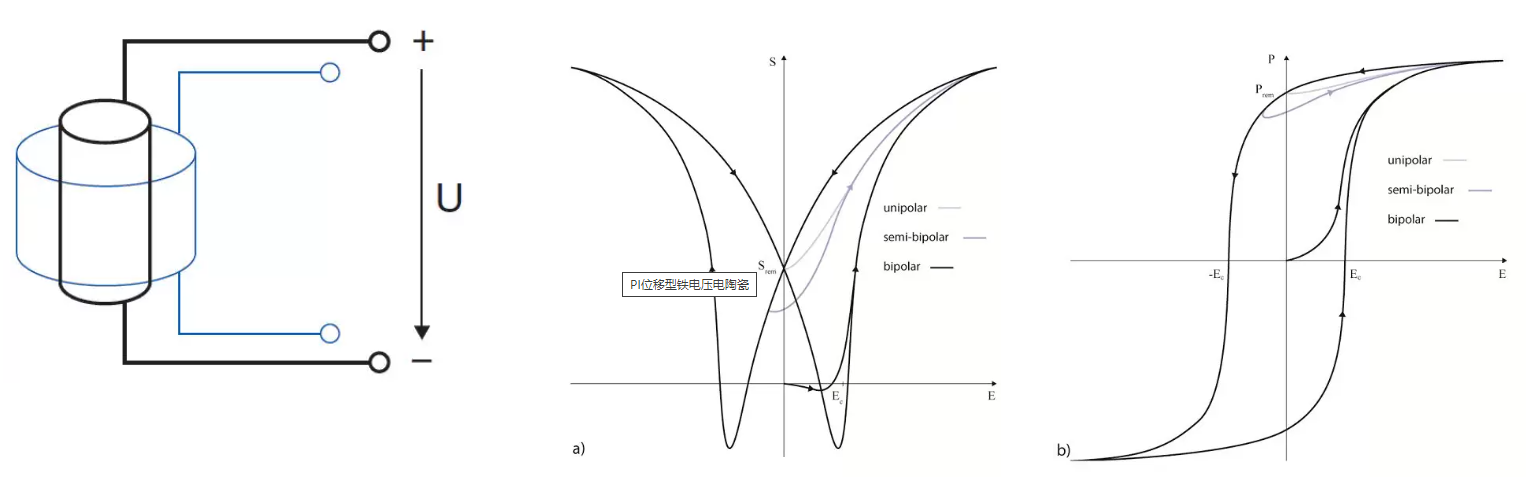
铁电压电陶瓷在不同控制振幅下的位移
机电
极化压电材料可由若干种系数和关系进行定性。
电气和弹性特性之间的基本关系可以用如下简化公式表示:
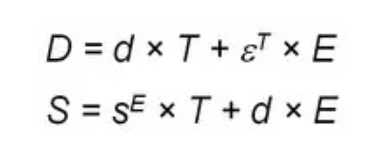
D :电通密度,T :机械应力;E:电场;S :机械应变;d :压电应变常数;εT :介电常数(T=常数);sE: 柔度或弹性系数(E=常数)
这些关系仅适用于较小的电气和机械振幅,即所谓的小信号值。在此范围内,机械、弹性变形S或应力T和电场E或电通量密度D之间是线性关系,系数值是常数。 可在材料数据表中找到这些小信号系数:
轴的分配
轴1、轴2和轴3(对应笛卡儿坐标系的X轴、Y轴和Z轴)表示方向,旋转轴(坐标系中的U、V和W)用4、5和6表示。 极化过程的产生是通过在两个电极之间施加一个强电场,极化方向(轴3)在此过程中被建立,且此时压电陶瓷能达到最大位移。 由于压电材料具有各向异性,相应的物理量通过张量进行描述,因而压电系数也通过相应指标表示。

用于描述极化压电陶瓷特征的正交系。轴3代表极化方向。
压电系数
弹性柔度sij
弹性柔度系数s是相对变形S与机械应力T的比值。机械能和电能互为依存,因而必须考虑电通量密度D和电场强度E等电磁边界条件。
示例: s33E恒定电场中方向3上的机械应变与方向3上的机械应力的比值(E = 0:短路) s55E恒定电介质位移下剪切应变与有效剪切应力的比值(D = 0:空载) 常用弹性或杨氏模量Yij大致对应相应弹性系数的倒数值。
频率系数Ni
频率系数N描述个体几何尺寸与相应(串联)谐振频率之间的关系。表示振动相应方向的指数:A = 尺寸,N = fS × A.
示例: N3细棒纵向振荡的频率系数,纵向方向上极化 N1细棒横向振荡的频率系数,方向3上极化 N5薄板沿厚度方向振荡的频率系数 NP圆盘沿平面方向振荡的频率系数 Nt厚度方向上极化的薄板沿厚度方向振荡的频率系数
机械品质因数Qm
机械品质因数Qm表示压电体或谐振器的“谐振锐度”,主要是由可振动系统串联谐振的3dB带宽决定。机械品质因数的倒数值是力学损耗因子,即压电谐振器共振时的等效电路图中有效电阻与电抗的比值。
耦合因子k
耦合因子k是衡量压电效应程度的标准(非效率因子)。它表示一种压电材料将电能与机械能相互转换的能力。耦合因子由储存机械能和总吸收能量的比值的平方根决定。谐振中,k是表示压电体振动的相应形式的函数。
示例:
k33纵向振荡的耦合因子
k31横向振荡的耦合因子
kP圆盘径向(平面)振荡的耦合因子
kt板材沿厚度方向振荡的耦合因子 k15板材沿厚度方向剪切振荡的耦合因子
介电常数ε
介电常数ε或相对介电系数DC是陶瓷材料的绝对介电常数和真空介电常数的比值(ε0 = 8.85 × 10-12 F/m),其中绝对介电常数是判断电场中极化率的标准。介电系数对电场方向和电介质位移的依赖性通过相应指标表示。
示例: ε33T 在极化方向(方向3)以固定的机械应力施加电场时极化方向的DC值(T=0:“自由空间”电容率) ε11S 定变形下轴1方向的电场和电介质位移(S=0:“受夹”电容率)
压电应变常数,压电变形系数,压电模量dij
压电模量是诱导电荷与机械应力或可实现的机械应力与施加电场的比值(T=常数)。对于压电促动器,压电模量也称为变形系数。 例如:d33极化方向上每单位施加电场产生的应变V/m或每单位压力N/m2下的电荷密度C/m2
压电电压系数gij
压电电压系数g是电场强度E与有效机械应力T的比值。各压电电荷系数dij除以相应的介电常数可得到相应的g ij系数。 示例: g31作用于方向1上每单位机械应力在方向3上的感应电场=单位面积上的力,不一定是正交
动态行为
激发振荡的压电体的机电特性可用电气等效电路图表示。 C0是指介质的电容。包含C1、L1和 R1的串联电路描述了弹性变形、有效质量(惯性)和内部摩擦产生的机械损失等机械性能的变化。然而,此振荡电路的描述仅适用于机械固有谐振附近的频率。大多数压电材料参数是通过对共振时的特殊试验体进行阻抗测量来确定。串联和并联共振都被用来确定压电参数,分别对应最小阻抗fm和最大阻抗fn的充分逼近值。
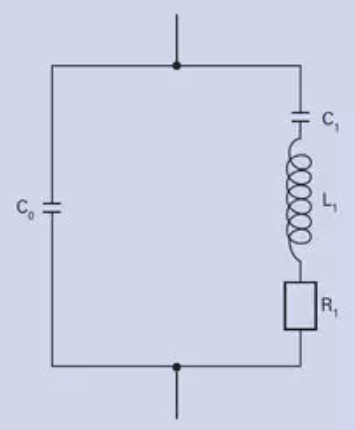
压电晶体谐振器的等效电路图
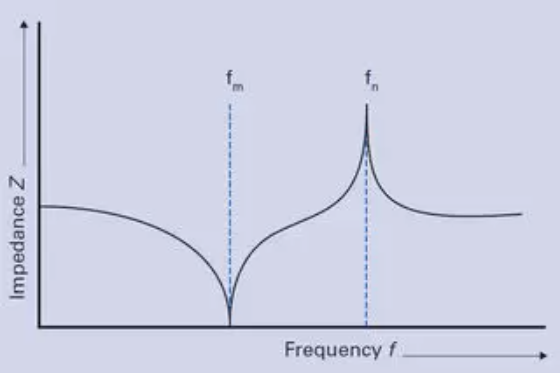
典型阻抗曲线
压电陶瓷元件的振荡状态
振荡状态或模式与变形是由个体的几何形状、机械-弹性特征以及电场和极化的方向决定的。
来源:PI Ceramic
原文链接:https://www.pi-china.cn/zh_cn/expertise/technology/piezo-technology/fundamentals
长按识别二维码关注公众号,点击下方菜单栏左侧“微信群”,申请加入交流群。

